Как рассчитать силу с помощью закона Гука — основы расчетов и примеры применения

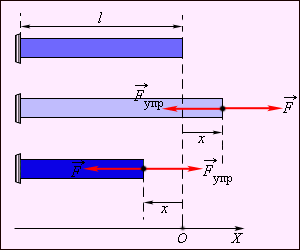
Закон Гука, или закон Гука-Лейбница, является одним из фундаментальных законов механики, который позволяет рассчитывать силу, действующую на упругое тело. Этот закон, названный в честь немецкого ученого Роберта Гука, сформулирован как: «Удлинение (сжатие) упругого стержня прямо пропорционально действующей на него силе, при условии, что упругий стержень не превышает своей предельной деформации».

Основными принципами закона Гука являются:

• Линейность. Закон Гука работает только для линейно упругих материалов, то есть для тех, которые при расчетах можно рассматривать как идеально упругие тела. Это означает, что упругое тело должно возвращаться к своей исходной форме после прекращения действия силы.
• Пропорциональность. Увеличение действующей силы на упругое тело ведет к увеличению его удлинения (сжатия) в точно таком же соотношении. Это значит, что закон Гука можно выразить математически с помощью уравнения F = kx, где F — сила, действующая на тело, k — коэффициент жесткости (показатель пружинной характеристики материала), x — удлинение (сжатие) тела.
• Предельная деформация. Закон Гука справедлив только вплоть до предельной деформации упругого тела. Если деформация превышает предел упругости, то закон Гука не верен и материал начинает проявлять пластичность или разрушаться.

Концепция закона Гука может быть применена во многих областях науки и техники. Он находит применение в строительстве, машиностроении, электронике, физике и других отраслях. Рассчитывая силу с помощью закона Гука, мы можем предсказать поведение упругого материала при определенных условиях и применить этот знакомый закон в решении различных инженерных задач и разработке новых технологий.

Основы и применение закона Гука

Согласно закону Гука, при малых деформациях упругого тела, внутренняя сила, возникающая в теле, пропорциональна его деформации. Формула закона Гука выглядит следующим образом:

F = k * Δl

Где:

• F — сила, действующая на упругое тело (в ньютонах);
• k — коэффициент упругости (в ньютонах на метр);
• Δl — изменение длины тела (в метрах).

Закон Гука широко применяется в различных областях науки и техники. Например, его используют при расчете пружин, упругих материалов, растяжения или сжатия конструкций.

Применение закона Гука позволяет рассчитать силу, которая будет действовать на упругое тело при заданной деформации. Для этого необходимо знать коэффициент упругости и изменение длины тела.

Однако, важно помнить, что закон Гука справедлив только в линейном режиме. Это означает, что при больших деформациях закон может не давать точный результат. Кроме того, в реальных условиях могут присутствовать другие факторы, влияющие на деформацию и силу.

Тем не менее, закон Гука остается важным инструментом для анализа упругого поведения различных материалов и использования их в различных конструкциях и механизмах.

Принципы использования закона Гука

Принципы использования закона Гука включают следующие элементы:

1. Уравнение загружения. Закон Гука может быть представлен в виде уравнения загружения: F = k * x, где F — сила, k — коэффициент упругости и x — деформация материала. Данное уравнение помогает рассчитывать силу, необходимую для достижения определенной деформации.
2. Коэффициент упругости. Коэффициент упругости (также известный как жесткость материала) является ключевым параметром при использовании закона Гука. Он определяет, насколько материал сопротивляется изменению своей формы при приложении силы. Чем выше коэффициент упругости, тем жестче материал.
3. Линейная зависимость. Закон Гука предполагает линейную зависимость между силой и деформацией. Это значит, что приложение удвоенной силы приведет к удвоенной деформации материала, а приложение тройной силы — к тройной деформации и т.д.
4. Предел прочности. Закон Гука применим до определенного предела прочности материала. При превышении этого предела, материал начинает демонстрировать нелинейные и необратимые деформации, что указывает на его повреждение или разрушение.

Примеры использования закона Гука включают расчеты напряжений и деформаций в пружинах, измерение жесткости материалов и оценку сил, действующих на конструкции. Знание принципов использования закона Гука позволяет инженерам и ученым анализировать и предсказывать поведение механических систем с большой точностью.

Зависимость силы от деформации

Закон Гука описывает зависимость силы, действующей на упругое тело, от его деформации. Согласно этому закону, сила, рассчитанная по формуле F = k * Δx, пропорциональна смещению Δx, которое вызвало деформацию, и коэффициенту пружности k.

Таким образом, закон Гука позволяет определить силу, которая возникает при упругой деформации тела. Это особенно полезно при изучении таких явлений, как растяжение или сжатие пружин, где сила зависит от относительного удлинения или сжатия пружины.

Необходимо отметить, что закон Гука справедлив только в пределах эластической деформации, то есть до того момента, когда тело возвращается в свое исходное состояние после прекращения воздействия силы. При превышении предела упругости тела начинает происходить пластическая деформация и закон Гука уже не применим.

Примером применения закона Гука может служить измерение упругости материала путем растяжения образца до определенного смещения и рассчет численного значения силы, действующей на образец. Это позволяет определить, насколько материал эластичен и как он реагирует на воздействие внешних сил.

Пропорциональность силы и удлинения

Закон Гука устанавливает пропорциональность между силой, действующей на упругое тело, и его удлинением. Согласно закону, сила, необходимая для растяжения или сжатия упругого тела, прямо пропорциональна удлинению или сжатию этого тела. Формула для расчета силы по закону Гука имеет вид:

F = k * Δl

где F — сила, действующая на тело, k — коэффициент упругости (характеризует жесткость материала), Δl — удлинение или сжатие тела.

Применение закона Гука часто встречается в различных сферах науки и техники. Он используется при проектировании пружин, балочных конструкций, измерении механических свойств материалов и в других случаях, когда необходимо учитывать деформацию упругих тел под действием внешних сил.

Расчет силы с помощью закона Гука может быть полезен, например, при определении максимальной нагрузки, которую может выдержать материал без разрушения, или при расчете упругой деформации системы.

Примеры расчетов по закону Гука

F — сила, действующая на упругое тело (ньютон);

k — коэффициент упругости (ньютон/метр);

x — деформация тела (метр).

Рассмотрим примеры расчетов по закону Гука:

Пример 1:

Упругая пружина имеет коэффициент упругости k = 100 Н/м. Растянув пружину на 0,1 м, определите силу F, необходимую для этого.

Решение:

Согласно закону Гука, сила F прямо пропорциональна деформации x. Используя формулу закона Гука, получим:

F = k * x

F = 100 Н/м * 0,1 м = 10 Н

Таким образом, для растяжения пружины на 0,1 м необходимо приложить силу 10 Н.

Пример 2:

Упругое тело имеет коэффициент упругости k = 50 Н/м. При приложении силы 30 Н тело деформируется на 0,2 м. Определите деформацию x упругого тела.

Решение:

Согласно закону Гука, деформация x прямо пропорциональна силе F. Используя формулу закона Гука, получим:

F = k * x

Известно, что F = 30 Н и k = 50 Н/м. Подставим их в формулу:

30 Н = 50 Н/м * x

x = 0,6 м

Таким образом, сила 30 Н вызывает деформацию 0,6 м упругого тела.

Расчеты по закону Гука позволяют определить силу, деформацию или коэффициент упругости упругого тела. Кроме пружин, закон Гука применяется для расчета упругости различных материалов, например, сталей, резиновых изделий и т.д. Правильное применение закона Гука позволяет предсказать поведение упругих тел в различных условиях нагрузки и деформации.

Расчет удлинения пружины при известной силе

Закон Гука позволяет рассчитать удлинение пружины, когда известна сила, действующая на нее. Уравнение для расчета удлинения выглядит следующим образом:

ΔL = F / k

Где:

• ΔL — удлинение пружины (измеряется в метрах);
• F — сила, действующая на пружину (измеряется в ньютонах);
• k — коэффициент упругости (измеряется в ньютонах/метр).

Чтобы рассчитать удлинение пружины при известной силе, необходимо знать коэффициент упругости данной пружины. Коэффициент упругости зависит от материала из которого изготовлена пружина и ее формы.

Например, предположим, что на пружину действует сила F = 10 Н и известно, что коэффициент упругости этой пружины равен k = 2 Н/м. Применяя уравнение из закон Гука, мы можем рассчитать удлинение пружины:

ΔL = 10 Н / 2 Н/м = 5 м

Таким образом, при силе 10 Н пружина удлинится на 5 метров.

Расчет силы, приложенной к упругому материалу, при известном удлинении

Причем, сила, действующая на упругий материал, направлена в противоположную сторону его удлинения. Из этого следует, что сила распределена равномерно по всей площади сечения материала.

Для расчета силы, можно использовать следующую формулу: F = k⋅Δl, где F — сила, приложенная к материалу, k — упругая постоянная материала и Δl — удлинение материала.

Приведенная формула позволяет определить силу, которую нужно приложить к упругому материалу для достижения заданного удлинения. Обратно, с помощью этой формулы можно определить удлинение материала при известной силе.

Дополнительно, можно использовать дополнительное уравнение для определения упругой постоянной материала: k = F/Δl. Это уравнение позволяет определить, насколько материал упругий и насколько сила будет меняться при изменении удлинения.

Расчет силы, приложенной к упругому материалу, является важным этапом в проектировании механических систем и материалов. Он позволяет предварительно оценить воздействие силы на материал и гарантировать его надежность и безопасность в работе.

Вопрос-ответ:

Какую силу рассчитывают с помощью закона Гука?

С помощью закона Гука рассчитывается сила, с которой деформируется упругое тело при приложении силы. Закон Гука утверждает, что деформация тела пропорциональна силе, приложенной к нему.

Какие основные принципы лежат в основе закона Гука?

Основные принципы, лежащие в основе закона Гука, включают пропорциональность между деформацией и силой, линейную зависимость между силой и удлинением упругого тела, а также обратную пропорциональность между силой и площадью поперечного сечения тела.

Как можно применить закон Гука для расчета силы?

Для расчета силы с использованием закона Гука необходимо знать модуль упругости материала тела, смещение или удлинение тела и площадь поперечного сечения тела. Формула для расчета силы по закону Гука выглядит следующим образом: F = k * Δx, где F — сила, k — модуль упругости, Δx — смещение или удлинение тела.

Как можно применить закон Гука для расчета удлинения тела?

Для расчета удлинения тела с использованием закона Гука необходимо знать модуль упругости материала тела, приложенную силу и площадь поперечного сечения тела. Формула для расчета удлинения тела по закону Гука выглядит следующим образом: Δx = (F / k) * L, где Δx — удлинение тела, F — приложенная сила, k — модуль упругости, L — исходная длина тела.

Как можно применить закон Гука для расчета модуля упругости?

Для расчета модуля упругости с использованием закона Гука необходимо знать приложенную силу, удлинение тела и площадь поперечного сечения тела. Формула для расчета модуля упругости по закону Гука выглядит следующим образом: k = (F / Δx) * (1 / L), где k — модуль упругости, F — приложенная сила, Δx — удлинение тела, L — исходная длина тела.

Какую силу рассчитывают с помощью закона Гука?

С помощью закона Гука можно рассчитать силу, действующую на упругое тело, когда оно подвергается деформации. Закон Гука описывает связь между силой и деформацией упругого тела.